Last updated: 27 May 2020
Amortised cost is the amount at which some financial assets or liabilities are measured and consists of:
- initial recognition amount,
- subsequent recognition of interest income/expense using the effective interest method,
- repayments and
- credit losses.
Let’s start with the two essential definitions set out in Appendix A to IFRS 9:
Effective interest rate (‘EIR’) is the rate that exactly discounts estimated future cash flows through the expected life of the financial asset/liability to the gross carrying amount of a financial asset or to the amortised cost of a financial liability. Gross carrying amount is the amortised cost of a financial asset before adjusting for any loss allowance.
Effective interest method is the method that is used in the calculation of the amortised cost of a financial asset/liability and in the allocation and recognition of the interest revenue or interest expense in P/L over the relevant period.
Illustration of application of amortised cost and effective interest method is presented below:
Example: Illustration of application of amortised cost and effective interest method
Entity A purchases a bond on a stock exchange for $900. All the relevant data for this example is presented below:
Face value: $1,000
Transaction price (incl. coupon accrued to date): $900
Transaction fee: $10
Coupon: 5%, that is $50 (calculated on face value, fixed and paid annually on 31 December)
Acquisition date: 20X1-05-01
Redemption date: 20X5-12-31
Based on the data above, Entity A is able to prepare a schedule for cash flows and calculate the effective interest rate (‘EIR’) as presented below. EIR can be calculated using spreadsheet function. In MS Excel, this can be done using ‘XIRR’ function.
All calculations presented in this example are available for download in an excel file.
Cash flows of the acquired bond give the EIR at 7.8%:
| date | cash flow |
|---|---|
| 20X1-05-01 | (900) |
| 20X1-05-01 | (10) |
| 20X1-12-31 | 50 |
| 20X2-12-31 | 50 |
| 20X3-12-31 | 50 |
| 20X4-12-31 | 50 |
| 20X5-12-31 | 50 |
| 20X5-12-31 | 1,000 |
| EIR | 7.8% |
Once EIR has been calculated, Entity A is able to calculate interest income for each year. The accounting schedule for this bond is as follows:
| year | acquisition date/ opening balance |
interest in P/L | cash flow | closing balance 31 Dec |
|---|---|---|---|---|
| 20X1 | 910 | 47 | (50) | 907 |
| 20X2 | 907 | 71 | (50) | 928 |
| 20X3 | 928 | 72 | (50) | 950 |
| 20X4 | 950 | 74 | (50) | 974 |
| 20X5 | 974 | 76 | (1,050) | – |
Note that you can scroll the table horizontally if it doesn’t fit your screen.
Expected cash flows
When calculating the effective interest rate (‘EIR’), an entity estimates the expected cash flows by considering all the contractual terms of the financial instrument, for example: prepayment, extension, call and similar options (see definition of EIR in Appendix A to IFRS 9 and paragraphs IFRS 9.BCZ5.65+ for more discussion).
As we can see from the above, EIR is based on estimated cash flows and there is a presumption that the cash flows and the expected life of a group of similar financial instruments can be estimated reliably. However, in those rare cases when it is not possible to reliably estimate the cash flows or the expected life of a financial instrument (or group of financial instruments), the entity uses the contractual cash flows over the full contractual term of the financial instrument (or group of financial instruments) (IFRS 9.Appendix A).
See also the impact of expected credit losses on interest calculation.
Revisions to and modifications of cash flows
Decision tree
Below is a decision tree regarding the accounting treatment of revisions to and modifications of cash flows in amortised cost calculation:
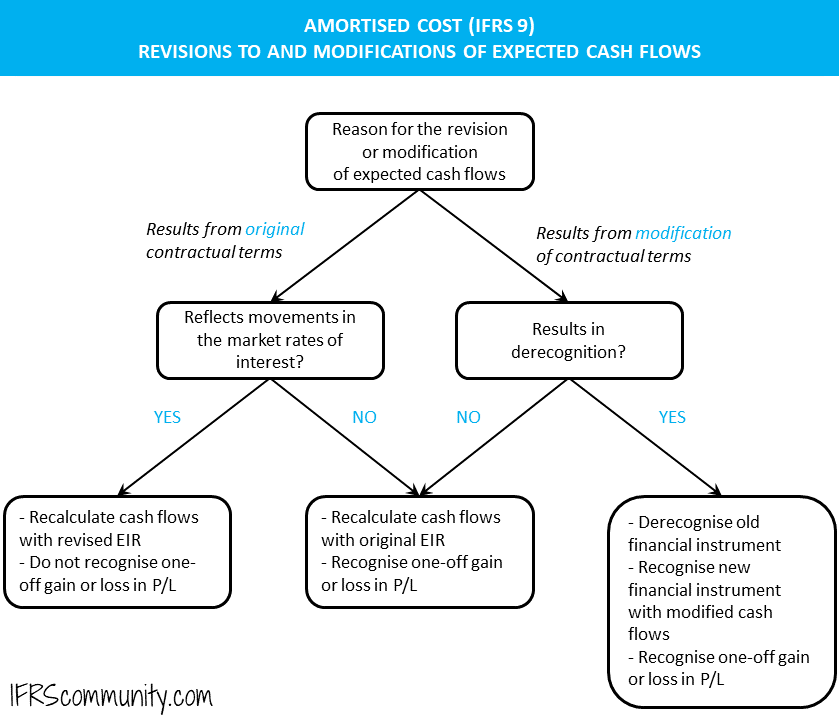
Movements in market interest rates
For floating-rate instruments, periodic re-estimation of cash flows impacts EIR without any one-off gain or loss in P/L. It is important to note that this approach applies to changes that reflect movements in the market rates of interest only. Other revisions made to cash flow estimates, even if they result from original contractual terms (e.g. increases in margin due to changes in borrower’s financial gearing ratio), will result in a different treatment as discussed below (IFRS 9.B5.4.5).
An example of accounting treatment for floating-rate instruments is given below.
Example: Re-estimation of cash flows for floating-rate instruments
Entity A purchases a bond on a stock exchange for $1,000. All the relevant data for this example is presented below:
Face value: $1,000
Transaction price: $1,000
Transaction fee: $0
Acquired interest: $25
coupon: 5% (LIBOR + 1p.p., paid and reset annually)
acquisition date: 20X1-07-01
redemption date: 20X5-12-31
Based on estimated cash flows, Entity A calculates effective interest rate (‘EIR’) at 5.0% (see a simple example for calculating EIR). All calculations presented in this example are available for download in an excel file. You can scroll the tables presented below horizontally if they don’t fit your screen.
Calculation of EIR based on current LIBOR:
| date | cash flow |
|---|---|
| 20X1-07-01 | (1,000) |
| 20X1-07-01 | (25) |
| 20X1-12-31 | 50 |
| 20X2-12-31 | 50 |
| 20X3-12-31 | 50 |
| 20X4-12-31 | 50 |
| 20X5-12-31 | 1,050 |
| EIR | 5.0% |
Note that an alternative method, where estimated cash flows are based on forward rates, is also allowed, though it is much less common in practice (IFRS 9 does not specify the approach to be used).
The initial accounting schedule for the bond is as follows:
| year | acquisition date/ opening balance |
interest in P/L | cash flow | closing balance 31 Dec |
|---|---|---|---|---|
| 20X1 | 1,025 | 25 | (50) | 1,000 |
| 20X2 | 1,000 | 50 | (50) | 1,000 |
| 20X3 | 1,000 | 50 | (50) | 1,000 |
| 20X4 | 1,000 | 50 | (50) | 1,000 |
| 20X5 | 1,000 | 50 | (1,050) | – |
Let’s now assume that the annual coupon is reset to 6% on 1 January 20X4 following an increase in LIBOR. As mentioned earlier, for floating-rate instruments, revisions to cash flows reflecting movements in market rates of interest affect the EIR without any one-off gain/loss in P/L (IFRS 9.B5.4.5). Therefore, Entity A calculates new EIR on 1 January 20X4 based on annual coupon at 6%:
| date | cash flows |
|---|---|
| 20X4-01-01 | (1,000) |
| 20X4-12-31 | 60 |
| 20X5-12-31 | 1,060 |
| EIR | 6.0% |
Note that the first negative cash flow shown on 20X4-01-01 is not an actual cash flow, but the amortised cost of the bond at the reset date. A negative opening value is necessary to calculate EIR in the spreadsheet.
The accounting schedule for the bond after increase in LIBOR is presented below:
| year | acquisition date/ opening balance |
interest in P/L | cash flow | closing balance 31 Dec |
|---|---|---|---|---|
| 20X4 | 1,000 | 60 | (60) | 1,000 |
| 20X5 | 1,000 | 60 | (1,060) | – |
As mentioned earlier, all calculations presented in this example are available in an excel file.
Other reasons for changes in expected cash flows under original contractual terms
When changes in expected cash flows are in line with original contractual terms, but they do not result from movements in market interest rates, an entity recalculates the amortised cost using financial instrument’s original effective interest rate (EIR). As a result, a one-off gain or loss is recognised in P/L (IFRS 9.B5.4.6). An example of this accounting treatment is presented below.
Example: Revision of cash flows in amortised cost calculation
Starting data for this example is identical as in this example. Entity A calculated EIR at 7.8% and prepared an accounting schedule for the acquired bond as follows (you can scroll these tables horizontally if they don’t fit your screen):
| year | acquisition date/ opening balance |
interest in P/L | cash flow | closing balance 31 Dec |
|---|---|---|---|---|
| 20X1 | 910 | 47 | (50) | 907 |
| 20X2 | 907 | 71 | (50) | 928 |
| 20X3 | 928 | 72 | (50) | 950 |
| 20X4 | 950 | 74 | (50) | 974 |
| 20X5 | 974 | 76 | (1,050) | – |
Let’s now assume that on 1 January 20X4, the issuer of this bond exercises a right to redeem the bond one year before its maturity, i.e. on 31 December 20X4 instead of 31 December 20X5. As we can see in the accounting schedule above, the amortised cost of this bond amounts to $950 on 1 January 20X4 (the date when Entity A makes revisions to expected cash flows). Entity A now expects to receive $1,050 on 31 December 20X4, which gives a present value of $974 ($1,050 discounted at original EIR of 7.8%). Therefore, Entity A increases the amortised cost of acquired bond by $24 and recognises a one-off gain in P/L (IFRS 9.B5.4.6). The accounting schedule for the bond, which takes into account the revision made to cash flows, is now as follows: (notice the additional column with one-off gain on revision).
All calculations presented in this example are available for download in an excel file.
| year | acquisition date/ opening balance |
one-off revision in P/L |
interest in P/L | cash flow | closing balance 31 Dec |
|---|---|---|---|---|---|
| 20X1 | 910 | – | 47 | (50) | 907 |
| 20X2 | 907 | – | 71 | (50) | 928 |
| 20X3 | 928 | – | 72 | (50) | 950 |
| 20X4 | 950 | 24 | 76 | (1,050) | – |
Modification of contractual terms that do not result in derecognition
The same approach as described above applies when contractual cash flows of a financial asset are renegotiated or otherwise modified, but without triggering derecognition of this asset (IFRS 9.5.4.3; B5.4.6). See also Example 11 accompanying IFRS 9.
The wording of paragraphs cited above may not be clear as to whether this rule applies to financial liabilities as well, but this was confirmed by the IASB in the basis for conclusions to IFRS 9 (BC4.252-3). Therefore, when a financial liability measured at amortised cost is modified without this modification resulting in derecognition, a gain or loss should be recognised in P/L. See the example of a modification of a financial liability not resulting in derecognition.
Modification of contractual terms resulting in derecognition
In some circumstances, renegotiation or modification of contractual cash flows can lead to derecognition of the existing financial asset (or liability) in accordance with IFRS 9. When the modification of a financial asset results in derecognition of the existing financial asset and the subsequent recognition of the modified financial asset, the modified asset is considered to be a ‘new’ financial asset. Accordingly, the date of the modification should be treated as the date of initial recognition of that asset, also when applying the impairment requirements (IFRS 9.B5.5.25-26).
Fees and other transaction costs
The calculation of effective interest rate includes all fees and points paid or received between parties to the contract that are an integral part of the effective interest rate, and includes also other transaction costs (IFRS 9.B5.4.1). Paragraphs IFRS 9.B5.4.2-3 give examples of fees that are, and are not, an integral part of the effective interest rate.
Fees relating to revolving credit facilities and other loan commitments are not part of the effective interest rate. As noted during one of the discussions on our Forum, a fee paid by the borrower is not specific to the amount borrowed. Therefore, it is simply recognised as an asset and amortised over the life of the credit facility. This treatment doesn’t change whether the borrower intends to drawdown or not. It is also important to note that loan commitments are generally out of scope of IFRS 9.
Amortisation of fees, premiums, discounts and similar items
Fees, premiums, discounts and similar items that are included in the calculation of the EIR are amortised over the expected life of the financial instrument, unless they relate to a shorter period. The shorter period is used when the variable to which the fees, transaction costs, premiums or discounts relate is repriced to market rates before the expected maturity of the financial instrument. For example, if a premium or discount on a floating-rate financial instrument reflects the interest that has accrued on that financial instrument since the interest was last paid, or changes in the market rates since the floating interest rate was reset to the market rates, it will be amortised to the next date when the floating interest is reset to market rates (IFRS 9.B5.4.4).
For financial instruments measured at FVTPL, fees are recognised in P/L in full when the instrument is initially recognised (IFRS 9.B5.4.1).
Credit-impaired financial assets
Purchased or originated credit-impaired financial assets are measured using credit-adjusted EIR. This means that initial ECL are included in the estimated cash flows when calculating EIR (IFRS 9.5.4.1(a);B5.4.7). More in the section on impact of expected credit losses on interest calculation.
More about financial instruments
See other pages relating to financial instruments:
Scope of IAS 32
Financial Instruments: Definitions
Derivatives and Embedded Derivatives: Definitions and Characteristics
Classification of Financial Assets and Financial Liabilities
Measurement of Financial Instruments
Amortised Cost and Effective Interest Rate
Impairment of Financial Assets
Derecognition of Financial Assets
Derecognition of Financial Liabilities
Factoring
Offsetting of Financial Instruments
Hedge Accounting
Financial Liabilities vs Equity
IFRS 7 Financial Instruments: Disclosures